Hamiltonian \(Q\)-Learning: Leveraging Importance-sampling for Data Efficient RL.

Udari Madhushani
Princeton Universiery
Biswadip Dey
Siemens
Naomi Leonard
Princeton Universiery
Amit Chakraborty
Siemens

Pdf Bibtex

Overview

Model-free reinforcement learning (RL), in particular \(Q\)-learning is widely used to learn optimal policies for a variety of planning and control problems. However, when the underlying state-transition dynamics are stochastic and high-dimensional, \(Q\)-Learning requires a large amount of data and incurs a prohibitively high computational cost. In this work, we introduce Hamiltonian \(Q\)-Learning, a data efficient modification of the \(Q\)-learning approach, which adopts an importance-sampling based technique for computing the \(Q\) function. To exploit stochastic structure of the state-transition dynamics, we employ Hamiltonian Monte Carlo to update \(Q\) function estimates by approximating the expected future rewards using \(Q\) values associated with a subset of next states. Further, to exploit the latent low-rank structure of the dynamic system, Hamiltonian \(Q\)-Learning uses a matrix completion algorithm to reconstruct the updated \(Q\) function from \(Q\) value updates over a much smaller subset of state-action pairs. By providing an efficient way to apply \(Q\)-learning in stochastic, high-dimensional problems, the proposed approach broadens the scope of RL algorithms for real-world applications, including classical control tasks and environmental monitoring.
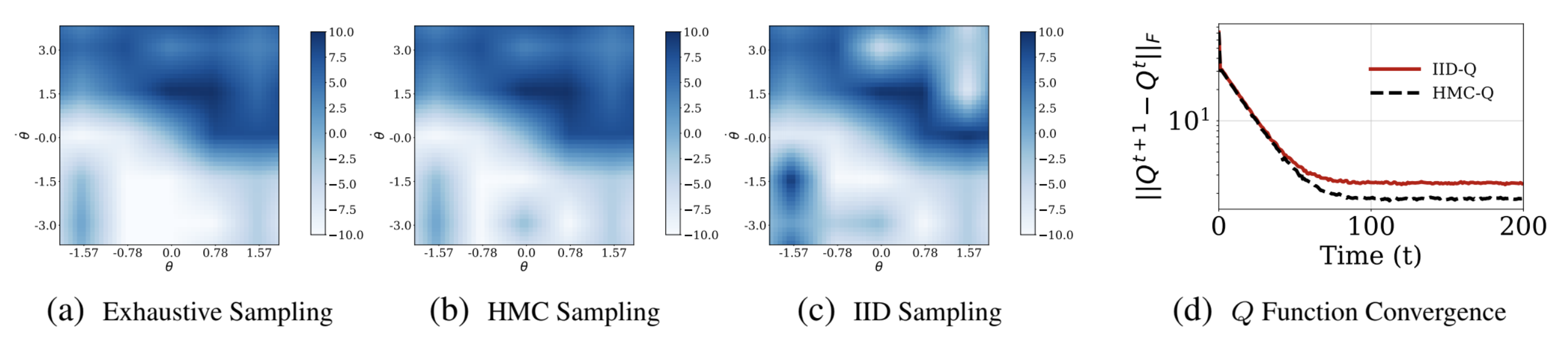
project
Results are provided for a cartpole system. Figures (a), (b) and (c) show policy heat maps for \(Q\)-Learning with exhaustive sampling, Hamiltonian \(Q\)-Learning and \(Q\)-Learning with IID sampling, respectively. Figure (d) provides a comparison for convergence of \(Q\) function with Hamiltonian \(Q\)-Learning and \(Q\)-Learning with IID sampling.

Application to adaptive ocean sampling

Ocean sampling plays a major role in a variety of science and engineering problems, ranging from modeling marine ecosystems to predicting global climate. Here, we consider the problem of using an under water glider to obtain measurements of a scalar field (e.g., temperature, salinity or concentration of a certain zooplankton) and illustrate how the use of Hamiltonian \(Q\)-Learning in planning the glider trajectory can lead to measurements that minimize the uncertainty associated with the field.
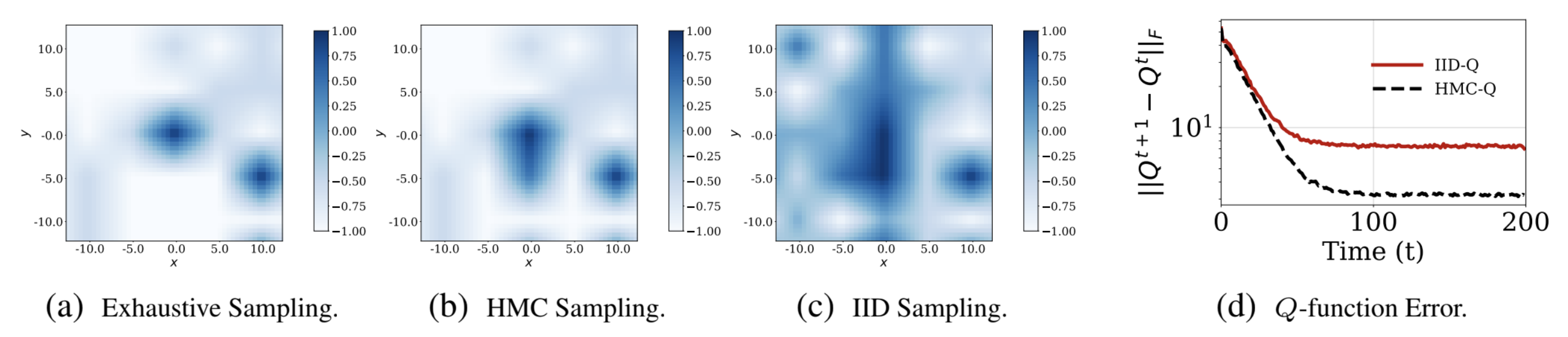
project
Figures (a), (b) and (c) show policy heat maps for \(Q\)-Learning with exhaustive sampling, Hamiltonian \(Q\)-Learning and \(Q\)-Learning with IID sampling, respectively. Figure (d) provides a comparison for convergence of \(Q\) function with Hamiltonian \(Q\)-Learning and \(Q\)-Learning with IID sampling.

Other related works

Bibtex

@article{madhushani2020QLearning,
  title={Hamiltonian Q-Learning: Leveraging Importance-sampling for Data Efficient RL},
  author={Madhushani, Udari and Dey, Biswadip and Leonard, Naomi Ehrich and Chakraborty, Amit},
  conference={under review},
  year={2020}
}