Overview
This work applies geometric PID control for asymptotic tracking of a desired trajectory by a hoop robot in the presence of disturbances and uncertainties. The hoop robot, consisting of a circular body rolling without slip along a one-dimensional surface, is a planar analog of a spherical robot. A variety of coupled mechanical system may be used to actuate the hoop robot. This paper specifically considers two different actuators, one a simple pendulum and the other an internal cart. The geometric PID controller requires the plant to be a simple mechanical system, and the hoop robot does not satisfy this condition. Therefore a geometric inner loop is presented that gives the hoop robot the required structure. This procedure is here referred to as feedback regularization. Feedback regularization—in contrast to feedback linearization—is coordinate independent, and hence reflects the fundamental system structure. Note also that the resulting mechanical system is nonlinear and underactuated. Subsequently, the geometric PID outer loop guarantees almost-semiglobal tracking with locally exponential convergence, and the integral action of the PID guarantees robustness to constant disturbances and parameter uncertainties, including constant inclination of the rolling surface. The complete tracking controller is the composition of the two coordinate-indep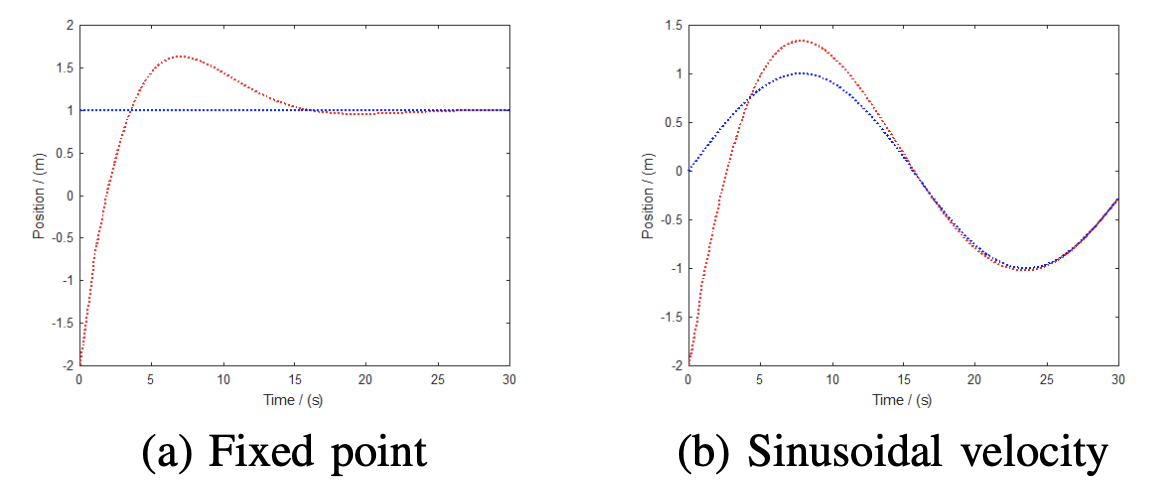
Numerical simulation results for a trajectory tracking hoop robot..
Bibtex
@inproceedings{madhushani2017feedback,
title={Feedback regularization and geometric pid control for trajectory tracking of mechanical systems: Hoop robots on an inclined plane},
author={Madhushani, TWU and Maithripala, DH Sanjeeva and Berg, Jordan M},
booktitle={2017 American Control Conference (ACC)},
pages={3938--3943},
year={2017},
organization={IEEE}
}